(미적분 참조 링크)
(빌) 15-3. 선적분의 기본 정리, 포텐셜 함수: https://0418cshyun.34
(빌) 16-1. 선형 적분과 비슷한 것 같은데… 표면 적분: https://0418cshyun.35
이 장에서 우리는 미적분학에서 이미 본 벡터 필드에 대해 이야기할 것입니다.
먼저 벡터장의 정의는 다음과 같다.
(벡터 필드)
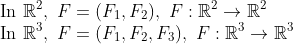
즉, 모든 유클리드 공간의 모든 점에 해당하는 벡터 함수를 말합니다.
다음 개념을 정의해 보겠습니다.
(그라디언트, 발산, 컬)
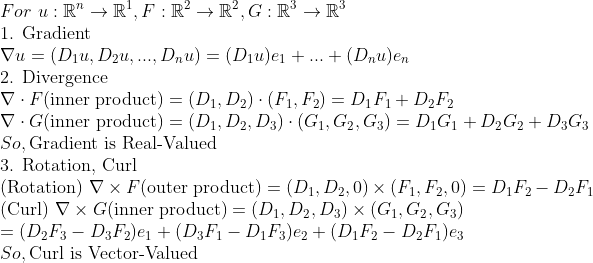
(미분 가능해야 하므로 모두 C1 매핑이라고 가정하자…)
(회전의 경우 컬과 같다고 생각하셔도 괜찮습니다! -> 방향은 z축 방향이지만…)
이러한 사실과 Stokes의 정리를 사용하여 다음 정리를 얻습니다.
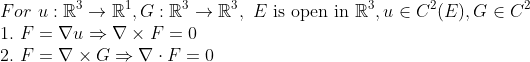
1. 잠재 함수가 존재하는 경우(정확한 형식) curl은 0입니다.
2. 컬의 발산은 항상 0입니다.
그 외에도 볼록 및 C2 등가 세트에서는 그 반대가 참입니다(즉, 닫힌 형식이 정확한 형식이면 그 반대도 참입니다).
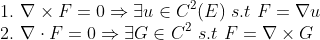
이러한 속성은 물리학에서 일반적으로 사용되므로 알고 있어야 합니다!
(입증하다)
3D일 때만 증명하라!
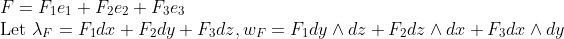
하나.
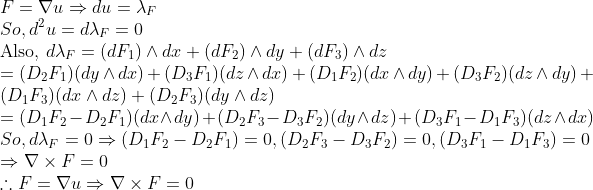
2.

위 미분형식의 미분과는 별개로 모든 요소를 비교하였기 때문에 요소비교는 그 반대가 될 수 있다.
요약하자면
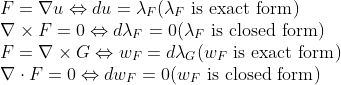
즉, 이전 장에서 만든 정확한 형식과 닫힌 형식의 관계일 뿐입니다!
따라서 볼록 집합과 C2 등가 집합 모두에 대해 반대가 성립합니다!
다음으로 살펴볼 것은 Green의 정리입니다. -> 2차원 벡터장에 대한 스토크스의 정리라고 생각하시면 됩니다!
(그린의 정리)
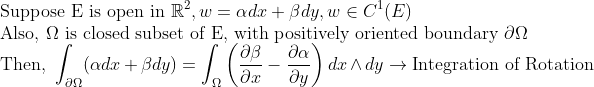
(입증하다)
Stokes의 정리를 사용하십시오.
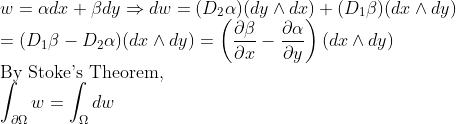
(그린의 정리 적용)
이것은 면적을 계산할 때 도움이 될 수 있습니다.

이 사실로 우리는 지역을 찾을 수 있습니다.
즉, 어떻게 든 회전 1을하자
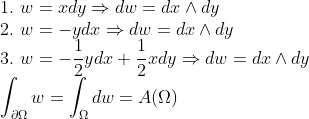
즉, 세 벡터 필드의 면적을 모두 보존할 수 있습니다!
dx^dy는 일종의 표면 요소 역할을 합니다. 이것을 3차원으로 확장하면 부피도 마찬가지입니다.
따라서 다음과 같이 Volume 요소를 정의해 보겠습니다.
(솔리드 요소)
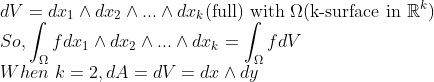
그럼 스톡스의 정리를 3차원 공간에서 이렇게 써봅시다.
그러나 3차원 공간이라면 문제가 조금 달라진다. 3차원 공간에 2차원 곡면이 존재할 수 있기 때문이다.
2차원 표면은 2-표면으로 정의할 수 있습니다.
(3D 표면)
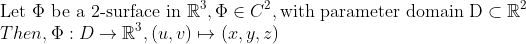
이 파이에 대해 다음 벡터 필드를 정의해 봅시다!
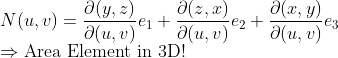
왜 이 n 표면 요소작동하는지 봅시다!
먼저 파이의 모든 점에 해당하는 점 (phi(p_0))에서 (1차 근사)에 접하는 평면(pi)을 만들어 봅시다!
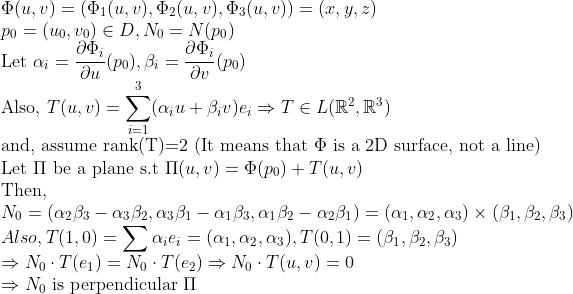
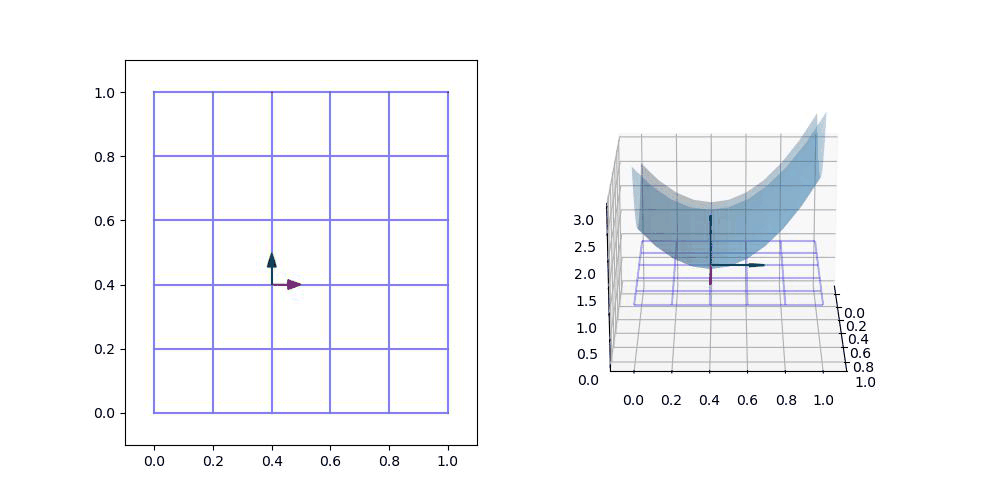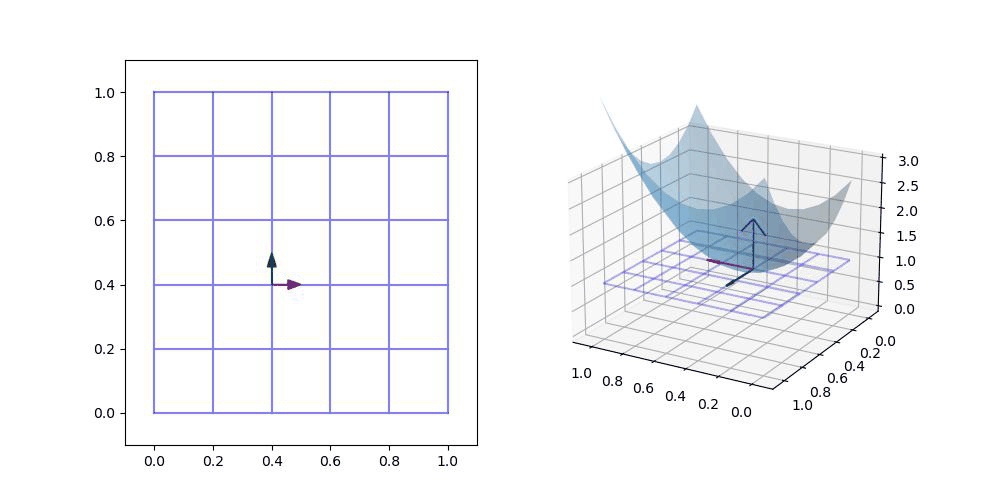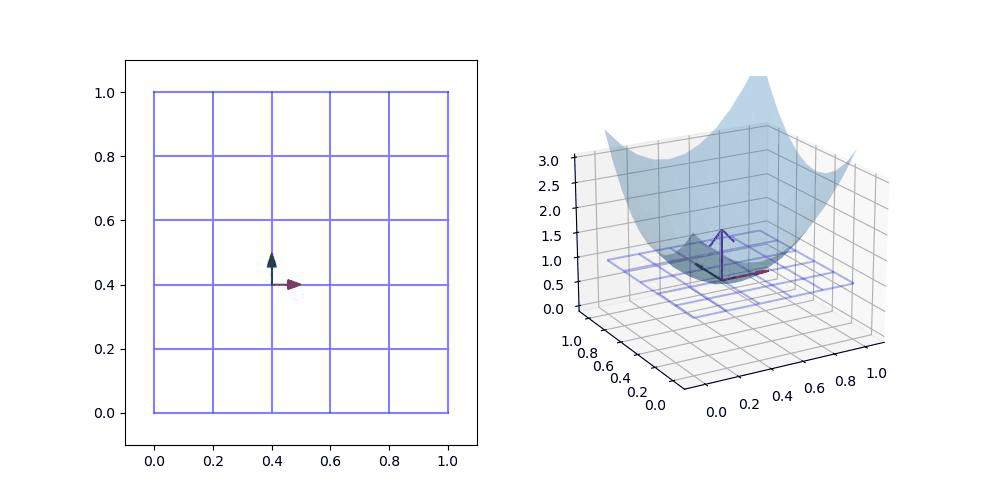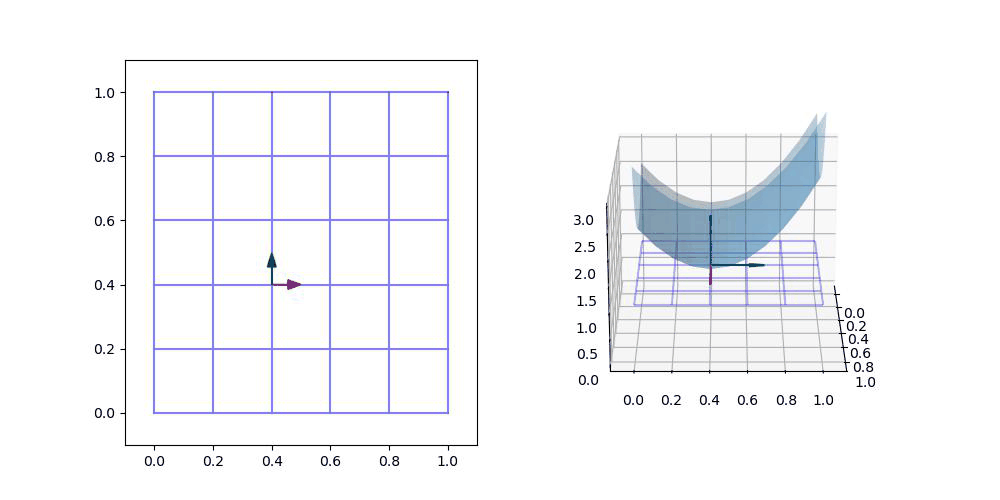
위에서 빨간색 화살표를 알파 벡터라고 하고 녹색 화살표를 베타 벡터라고 부를 수 있습니다!
(참고. 오른쪽의 알파 및 베타 벡터는 서로 수직일 필요가 없습니다!)
1. 모든 p_0에 적용해야 하므로, 표면의 모든 점에서 N은 접평면에 수직입니다!
2. 또한 외적의 종류에 따라 N_0의 크기는 알파 벡터와 베타 벡터가 이루는 평행사변형의 면적과 같다.
-> 즉 N_0의 크기는 해당 점(p_0)에서 접하지 않는 평면의 면적입니다.당신은 말할 수 있습니다!
이런 이유로
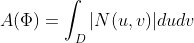
당신이 무슨 말을하든 상관 없습니다!
3. 긍정적 지향!
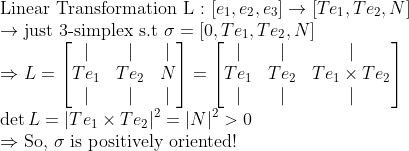
즉, Standard Simplex의 축은 서로 바뀌지 않습니다! (회전시 표준 단방향 좌표축 순서와 일치)
—-> 그러므로 표면 적분다음과 같이 정의할 수 있습니다.
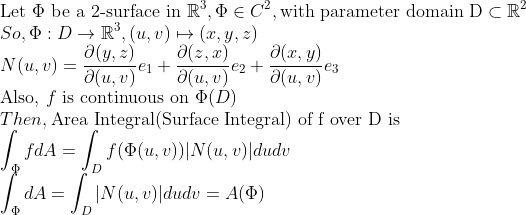
여기까지 설명을 따라오셨다면 어렵지 않게 이해할 수 있을 것입니다.
우선 지금까지 스토크스의 정리를 2차원 -> 그린의 정리,
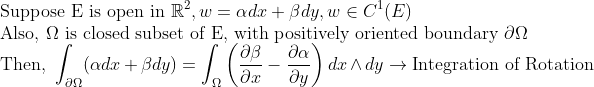
(Stokes’ 정리에 의해 왼쪽이 1면 1형 / 반대쪽이 2면 2형) -> (k=2,m=2)
이것을 3D 공간으로 확장하려고 했지만 이 시점에서 스코프 콘텐츠가 나타났습니다.
즉 위와 같이 (1면 1자형 / 2면 2자형) 원하는데 문제는 3D그만큼…
(스토크스 정리에서 k=2, m=3만약에…)
다음 장에서 3D 공간에서 진화하는 방법을 보자!
