문제 설명
명함 지갑을 만드는 회사가 지갑의 크기를 결정하려고 합니다. 모든 모양과 크기의 명함을 담을 수 있으면서도 작고 휴대하기 편리한 지갑을 만들어야 합니다. 이러한 요구 사항을 충족하는 지갑을 만들기 위해 디자인 팀은 모든 명함의 너비와 높이를 연구했으며 아래 표는 4장의 명함 너비와 높이를 보여줍니다.가장 긴 가로 세로 길이가 각각 80, 세로 70이므로 80(가로) x 70(세로) 크기의 지갑을 만들면 모든 명함을 수납할 수 있습니다. 단, 2번 명함을 가로로 수납할 경우 80(가로) x 50(세로) 지갑 하나에 모든 명함을 넣을 수 있습니다. 이때 지갑 크기는 4000(=80 x 50)입니다.
모든 명함의 가로 세로 길이를 나타내는 2차원 필드 크기를 매개변수로 지정합니다. 모든 명함을 담을 수 있는 가장 작은 지갑을 만들면 풀이 함수를 완성하여 지갑의 크기를 반환합니다.제한
수량의 길이는 1보다 크거나 같고 10,000보다 작거나 같습니다.
크기 요소의 형식은 (w, h)입니다.
w는 명함의 가로 길이를 나타냅니다.
h는 명함의 세로 길이를 나타냅니다.
w 및 h는 1 이상 1,000 이하의 자연수이다.I/O 예시 설명
I/O 예제 문제 1번 예제와 동일합니다.
입력/출력 예제 #2 명함이 제대로 회전되어 쌓이면 세 번째 카드(너비: 8, 높이: 15)가 다른 모든 카드보다 큽니다. 따라서 지갑의 크기는 세 번째 명함의 크기와 같으며 120(=8 x 15)을 반환합니다.
입력/출력 예제 #3 명함을 제대로 회전하고 겹쳤을 때 모든 명함을 담는 가장 작은 지갑의 크기는 133(= 19 x 7)입니다.
논평
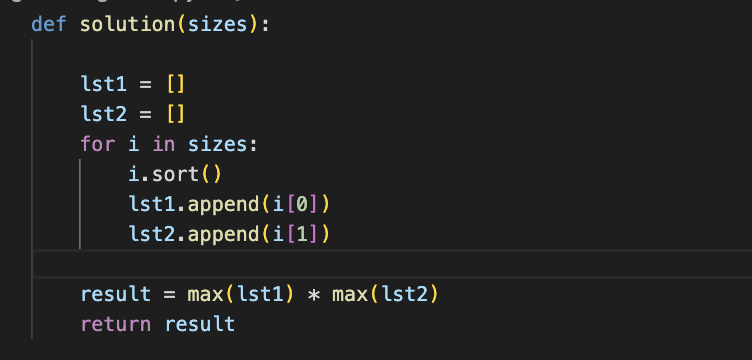
크기((10, 7), (12, 3), (8, 15), (14, 7), (5, 15))
나는 이것을 가지고있다 ((7, 10), (3, 12), (8, 15), (7, 14), (5, 15)) 이렇게 하면 목록에서 작은 숫자가 인덱스(0)로 이동하고 큰 숫자가 인덱스(1)로 이동합니다.
그 이유는 수직 및 수평 크기가 궁극적으로 가장 큰 명함이 아닌 모든 명함을 포함하는 직사각형이기 때문입니다.
따라서 목록 요소가 정렬됩니다.
lst1 및 lst2에 요소 0과 1을 포함합니다.
그렇게 표현하면
lst1 = (7, 3, 8, 7, 5)
lst2 = (10, 12, 15, 14, 15)
이렇게 표기되어 있습니다
각 목록에서 가장 큰 요소를 곱합니다.
